Young measure

In mathematical analysis, a Young measure is a parameterized measure that is associated with certain subsequences of a given bounded sequence of measurable functions. Young measures have applications in the calculus of variations and the study of nonlinear partial differential equations. They are named after Laurence Chisholm Young.

Definition

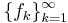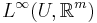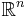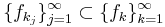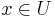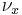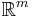We let $\{ f_k \}_{k=1}^\infty$ be a bounded sequence in $L^\infty (U,\mathbb{R}^m)$ , where $U$ denotes an open bounded subset of $\mathbb{R}^n$ . 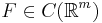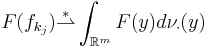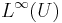Then there exists a subsequence $\{ f_{k_j} \}_{j=1}^\infty \subset \{ f_k \}_{k=1}^\infty$ and for almost every $x \in U$ a Borel probability measure $\nu_x$ on $\mathbb{R}^m$ such that for each $F \in C(\mathbb{R}^m)$ we have $F(f_{k_j}) \overset{\ast}{\rightharpoonup} \int_{\mathbb{R}^m} F(y)d\nu_\cdot(y)$ in $L^\infty (U)$ . 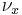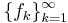The measures $\nu_x$ are called the Young measures generated by the sequence $\{ f_k \}_{k=1}^\infty$ .

Example

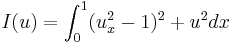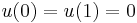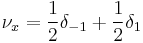Every minimizing sequence of $I(u) = \int_0^1 (u_x^2-1)^2 %2B u^2dx$ subject to $u(0)=u(1)=0$ generates the Young measures $\nu_x= \frac{1}{2} \delta_{-1} %2B \frac{1}{2}\delta_1$ .

This captures the essential features of all minimizing sequences to this problem, namely developing finer and finer slopes of 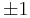$\pm 1$ .

References

L.C. Evans (1990). Weak convergence methods for nonlinear partial differential equations. Regional conference series in mathematics. American Mathematical Society.

Stefan Müller (1999). Variational models for microstructure and phase transitions. Lecture Notes in Mathematics. Springer.